RCD

Model

This method RCD (Repetitive Causal Discovery) [3]　assumes an extension of the basic LiNGAM model [1] to hidden common cause cases, i.e., the latent variable LiNGAM model [2]. Similarly to the basic LiNGAM model [1], this method makes the following assumptions:

Linearity
Non-Gaussian continuous error variables
Acyclicity

However, RCD allows the existence of hidden common causes. It outputs a causal graph where a bi-directed arc indicates the pair of variables that have the same hidden common causes, and a directed arrow indicates the causal direction of a pair of variables that are not affected by the same hidden common causes.

References

[1] (1,2)
S. Shimizu, P. O. Hoyer, A. Hyvärinen, and A. J. Kerminen. A linear non-gaussian acyclic model for causal discovery. Journal of Machine Learning Research, 7:2003-2030, 2006.

[2]
P. O. Hoyer, S. Shimizu, A. Kerminen, and M. Palviainen. Estimation of causal effects using linear non-gaussian causal models with hidden variables. International Journal of Approximate Reasoning, 49(2): 362-378, 2008.

[3]
T. N. Maeda and S. Shimizu. RCD: Repetitive causal discovery of linear non-Gaussian acyclic models with latent confounders. In Proc. 23rd International Conference on Artificial Intelligence and Statistics (AISTATS2020), Palermo, Sicily, Italy. PMLR 108:735-745, 2020.

Import and settings

In this example, we need to import numpy, pandas, and graphviz in addition to lingam.

import numpy as np
import pandas as pd
import graphviz
import lingam
from lingam.utils import print_causal_directions, print_dagc, make_dot

print([np.__version__, pd.__version__, graphviz.__version__, lingam.__version__])

np.set_printoptions(precision=3, suppress=True)

['1.24.4', '2.0.3', '0.20.1', '1.8.3']

Test data

First, we generate a causal structure with 7 variables. Then we create a dataset with 5 variables from x0 to x4, with x5 and x6 being the latent variables.

np.random.seed(0)

get_external_effect = lambda n: np.random.normal(0.0, 0.5, n) ** 3
n_samples = 300

x5 = get_external_effect(n_samples)
x6 = get_external_effect(n_samples)
x1 = 0.6*x5 + get_external_effect(n_samples)
x3 = 0.5*x5 + get_external_effect(n_samples)
x0 = 1.0*x1 + 1.0*x3 + get_external_effect(n_samples)
x2 = 0.8*x0 - 0.6*x6 + get_external_effect(n_samples)
x4 = 1.0*x0 - 0.5*x6 + get_external_effect(n_samples)

# The latent variable x6 is not included.
X = pd.DataFrame(np.array([x0, x1, x2, x3, x4, x5]).T, columns=['x0', 'x1', 'x2', 'x3', 'x4', 'x5'])

X.head()

	x0	x1	x2	x3	x4	x5
0	-0.191493	-0.054157	0.014075	-0.047309	0.016311	0.686190
1	-0.967142	0.013890	-1.115854	-0.035899	-1.254783	0.008009
2	0.527409	-0.034960	0.426923	0.064804	0.894242	0.117195
3	1.583826	0.845653	1.265038	0.704166	1.994283	1.406609
4	0.286276	0.141120	0.116967	0.329866	0.257932	0.814202

m = np.array([[ 0.0, 1.0, 0.0, 1.0, 0.0, 0.0, 0.0],
              [ 0.0, 0.0, 0.0, 0.0, 0.0, 0.6, 0.0],
              [ 0.8, 0.0, 0.0, 0.0, 0.0, 0.0,-0.6],
              [ 0.0, 0.0, 0.0, 0.0, 0.0, 0.5, 0.0],
              [ 1.0, 0.0, 0.0, 0.0, 0.0, 0.0,-0.5],
              [ 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0],
              [ 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0]])
dot = make_dot(m, labels=['x0', 'x1', 'x2', 'x3', 'x4', 'x5', 'f1(x6)'])

# Save pdf
dot.render('dag')

# Save png
dot.format = 'png'
dot.render('dag')

dot

Causal Discovery

To run causal discovery, we create a RCD object and call the fit method.

model = lingam.RCD()
model.fit(X)

<lingam.rcd.RCD at 0x7f76b338e8b0>

Using the ancestors_list_ properties, we can see the list of ancestors sets as a result of the causal discovery.

ancestors_list = model.ancestors_list_

for i, ancestors in enumerate(ancestors_list):
    print(f'M{i}={ancestors}')

M0={1, 3, 5}
M1={5}
M2={0, 1, 3, 5}
M3={5}
M4={0, 1, 3, 5}
M5=set()

Also, using the adjacency_matrix_ properties, we can see the adjacency matrix as a result of the causal discovery. The coefficients between variables with latent confounders are np.nan.

model.adjacency_matrix_

array([[0.   , 0.939, 0.   , 0.994, 0.   , 0.   ],
       [0.   , 0.   , 0.   , 0.   , 0.   , 0.556],
       [0.751, 0.   , 0.   , 0.   ,   nan, 0.   ],
       [0.   , 0.   , 0.   , 0.   , 0.   , 0.563],
       [1.016, 0.   ,   nan, 0.   , 0.   , 0.   ],
       [0.   , 0.   , 0.   , 0.   , 0.   , 0.   ]])

make_dot(model.adjacency_matrix_)

Independence between error variables

To check if the LiNGAM assumption is broken, we can get p-values of independence between error variables. The value in the i-th row and j-th column of the obtained matrix shows the p-value of the independence of the error variables \(e_i\) and \(e_j\).

p_values = model.get_error_independence_p_values(X)
print(p_values)

[[0.    0.      nan 0.413   nan 0.68 ]
 [0.    0.      nan 0.732   nan 0.382]
 [  nan   nan 0.      nan   nan   nan]
 [0.413 0.732   nan 0.      nan 0.054]
 [  nan   nan   nan   nan 0.      nan]
 [0.68  0.382   nan 0.054   nan 0.   ]]

Bootstrapping

We call bootstrap() method instead of fit(). Here, the second argument specifies the number of bootstrap sampling.

import warnings
warnings.filterwarnings('ignore', category=UserWarning)

model = lingam.RCD()
result = model.bootstrap(X, n_sampling=100)

Causal Directions

Since BootstrapResult object is returned, we can get the ranking of the causal directions extracted by get_causal_direction_counts() method. In the following sample code, n_directions option is limited to the causal directions of the top 8 rankings, and min_causal_effect option is limited to causal directions with a coefficient of 0.01 or more.

cdc = result.get_causal_direction_counts(n_directions=8, min_causal_effect=0.01, split_by_causal_effect_sign=True)

We can check the result by utility function.

print_causal_directions(cdc, 100)

x4 <--- x0 (b>0) (58.0%)
x0 <--- x5 (b>0) (51.0%)
x2 <--- x0 (b>0) (30.0%)
x3 <--- x5 (b>0) (30.0%)
x0 <--- x1 (b>0) (22.0%)
x0 <--- x3 (b>0) (18.0%)
x1 <--- x5 (b>0) (18.0%)
x2 <--- x5 (b>0) (15.0%)

Directed Acyclic Graphs

Also, using the get_directed_acyclic_graph_counts() method, we can get the ranking of the DAGs extracted. In the following sample code, n_dags option is limited to the dags of the top 3 rankings, and min_causal_effect option is limited to causal directions with a coefficient of 0.01 or more.

dagc = result.get_directed_acyclic_graph_counts(n_dags=3, min_causal_effect=0.01, split_by_causal_effect_sign=True)

We can check the result by utility function.

print_dagc(dagc, 100)

DAG[0]: 6.0%
DAG[1]: 4.0%
    x4 <--- x0 (b>0)
DAG[2]: 4.0%
    x2 <--- x0 (b>0)

Probability

Using the get_probabilities() method, we can get the probability of bootstrapping.

prob = result.get_probabilities(min_causal_effect=0.01)
print(prob)

[[0.   0.22 0.   0.18 0.   0.51]
 [0.   0.   0.   0.   0.   0.18]
 [0.3  0.13 0.   0.12 0.05 0.15]
 [0.   0.   0.   0.   0.   0.3 ]
 [0.58 0.11 0.02 0.11 0.   0.05]
 [0.   0.   0.   0.   0.   0.  ]]

Total Causal Effects

Using the get_total_causal_effects() method, we can get the list of total causal effect. The total causal effects we can get are dictionary type variable. We can display the list nicely by assigning it to pandas.DataFrame. Also, we have replaced the variable index with a label below.

causal_effects = result.get_total_causal_effects(min_causal_effect=0.01)

# Assign to pandas.DataFrame for pretty display
df = pd.DataFrame(causal_effects)
labels = [f'x{i}' for i in range(X.shape[1])]
df['from'] = df['from'].apply(lambda x : labels[x])
df['to'] = df['to'].apply(lambda x : labels[x])
df

	from	to	effect	probability
0	x3	x0	1.055784	0.04
1	x3	x2	0.818606	0.04
2	x4	x2	0.484138	0.04
3	x3	x4	1.016508	0.04
4	x1	x0	0.929668	0.03
5	x0	x2	0.781983	0.03
6	x0	x4	1.003733	0.03
7	x1	x4	1.041410	0.03
8	x1	x2	0.730836	0.02
9	x5	x0	0.961161	0.01
10	x5	x1	0.542628	0.01
11	x5	x3	0.559532	0.01

We can easily perform sorting operations with pandas.DataFrame.

df.sort_values('effect', ascending=False).head()

	from	to	effect	probability
0	x3	x0	1.055784	0.04
7	x1	x4	1.041410	0.03
3	x3	x4	1.016508	0.04
6	x0	x4	1.003733	0.03
9	x5	x0	0.961161	0.01

df.sort_values('probability', ascending=True).head()

	from	to	effect	probability
9	x5	x0	0.961161	0.01
10	x5	x1	0.542628	0.01
11	x5	x3	0.559532	0.01
8	x1	x2	0.730836	0.02
4	x1	x0	0.929668	0.03

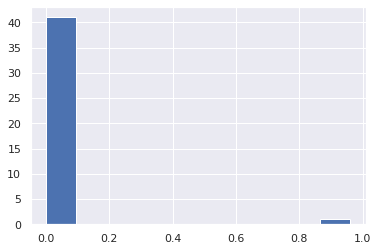
Because it holds the raw data of the causal effect (the original data for calculating the median), it is possible to draw a histogram of the values of the causal effect, as shown below.

import matplotlib.pyplot as plt
import seaborn as sns
sns.set()
%matplotlib inline

from_index = 5 # index of x5
to_index = 0 # index of x0
plt.hist(result.total_effects_[:, to_index, from_index])

Bootstrap Probability of Path

Using the get_paths() method, we can explore all paths from any variable to any variable and calculate the bootstrap probability for each path. The path will be output as an array of variable indices. For example, the array [3, 0, 1] shows the path from variable X3 through variable X0 to variable X1.

from_index = 5 # index of x5
to_index = 4 # index of x4

pd.DataFrame(result.get_paths(from_index, to_index))

	path	effect	probability
0	[5, 0, 4]	0.970828	0.34
1	[5, 3, 0, 4]	0.522827	0.07
2	[5, 3, 4]	0.461104	0.06
3	[5, 4]	0.821702	0.05
4	[5, 1, 0, 4]	0.605828	0.02
5	[5, 1, 4]	0.574573	0.02